数理统计——基本概念与先导知识

基本概念

• 样本：通过试验获得的数据，统计模拟中，生成的n个服从i.i.d的正态分布的点，就叫做n个样本，由于n个互相独立，我们也可以拿联合密度函数刻画。
• 参数：出现在样本中的未知常数。
• 讨厌参数：我们不感兴趣不研究，但是也会影响我们的参数。
• 参数空间：形如$\Theta =\{(\mu ,\sigma )\}$表示两参数的范围
• 统计量：对于样本$X_1,...,X_n$ ,有函数$T=T(X_1,...,X_n)$ 其中$T$与参数无关则可以称其为一个统计量。

有统计量的原因是因为样本本身是没有任何信息的，我们需要构建统计量帮助我们量化样本的信息，比如说对于一个$U(0,\theta )$的均匀分布，我们对于样本$X_1,...,X_n$很容易的到一个统计量$\bar{X}$ 我们可以用它来估计均匀分布的均值，也可以感性的用$2\bar{X}$来估计未知参数$\theta$，构造统计量可以帮助我们联系样本与感兴趣的内容。

先导知识（矩相关知识）

样本$k$阶矩

• 样本$k$阶原点矩：$a_k=\frac{1}{n}{\sum }_{i=1}^n{X}_i^k$
• 样本$k$阶中心距：$b_k=\frac{1}{n}{\sum }_{i=1}^n(X_i-\bar{X}{)}^k$

特别的，当$k$取1和2是与样本均值和样本方差有关

样本均值：

$\bar{x}=\frac{1}{n}{\sum }_{i=1}^n{x}_i$

• ${\sum }_{i=1}^n(x_i-\bar{x})=0$
• $\text{对于任意 }c,{\sum }_{i=1}^n(x_i-\bar{x}{)}^2\le {\sum }_{i=1}^n(x_i-c{)}^2.$
• $\text{若总体 }E(X)=\mu ,\mathrm{Var}(X)={\sigma }^2<\infty ,\text{则 }E(\bar{X})=\mu ,\mathrm{Var}(\bar{X})=\frac{1}{n}{\sigma }^2.$
• 若总体$X\sim N(\mu ,{\sigma }^2)$,则$\bar{X}\sim N(\mu ,{\sigma }^2/n)$,若总体分布未知或非正态分布$E(X)=\mu$,Var$(X)={\sigma }^2$存在，则$n$较大时，$\bar{X}$的渐进分布$N(\mu ,{\sigma }^2/n)$为并记为 $\bar{X}\sim N(\mu ,{\sigma }^2/n).$

证明过程都相对显然，我这里只给出TH2的证明 TH2：

$$\begin{array}{c}\begin{array}{rl}\sum _{i=1}^n(x_i-c{)}^2& =\sum _{i=1}^n(x_i-\overline{x}+\overline{x}-c{)}^2\\ & =\sum _{i=1}^n(x_i-\overline{x}{)}^2+2(\overline{x}-c)\sum _{i=1}^n(x_i-\overline{x})+n(\overline{x}-c{)}^2\\ & =\sum _{i=1}^n(x_i-\overline{x}{)}^2+n(\bar{x}-c{)}^2\ge \sum _{i=1}^n(x_i-\overline{x}{)}^2\end{array}\end{array}$$

可以看到，当且仅当$c=\bar{x}$时等号成立，这种操作，在后面也会遇到。

样本方差

$s^2=\frac{1}{n-1}{\sum }_{i=1}^n(x_i-\overline{x}{)}^2$

• 样本标准差$s=\sqrt{s^2}$
• 若总体方差${\sigma }^2<\infty$则$E[s^2]={\sigma }^2$ ,为无偏估计
• 样本标准差不是$\sigma$的无偏估计，$E[s]\ne \sigma$ (平方不保持线性)

样本偏度与峰度

• 样本偏度:从定义上来看，是样本的三阶标准化矩 $E\left[{\left(\frac{X-\mu }{\sigma }\right)}^3\right]=\frac{\mathrm{E}\left[(\mathrm{X}-\mu {)}^3\right]}{{\left(\mathrm{E}\left[(\mathrm{X}-\mu {)}^2\right]\right)}^{3/2}}$ 然后利用样本的$k$阶矩进行替换后可以的到样本的峰度表达式

$$\frac{\sqrt{n}{\sum }_{i=1}^n(x_i-\overline{x}{)}^3}{[{\sum }_{i=1}^n(x_i-\overline{x}{)}^2{]}^{\frac{3}{2}}}$$

• 样本峰度：样本的四阶标准化矩，同理可得

$$\frac{n{\sum }_{i=1}^n(x_i-\overline{x}{)}^4}{[{\sum }_{i=1}^n(x_i-\overline{x}{)}^2{]}^2}-3$$

由于在推导过程中用到样本矩，所以也可以利用样本矩进行记忆此时有

• 样本偏度

$${\hat{\beta }}_s=\frac{b_3}{b_2^{\frac{3}{2}}}$$

• 样本峰度

$${\hat{\beta }}_k=\frac{b_4}{b_2^2}-3$$

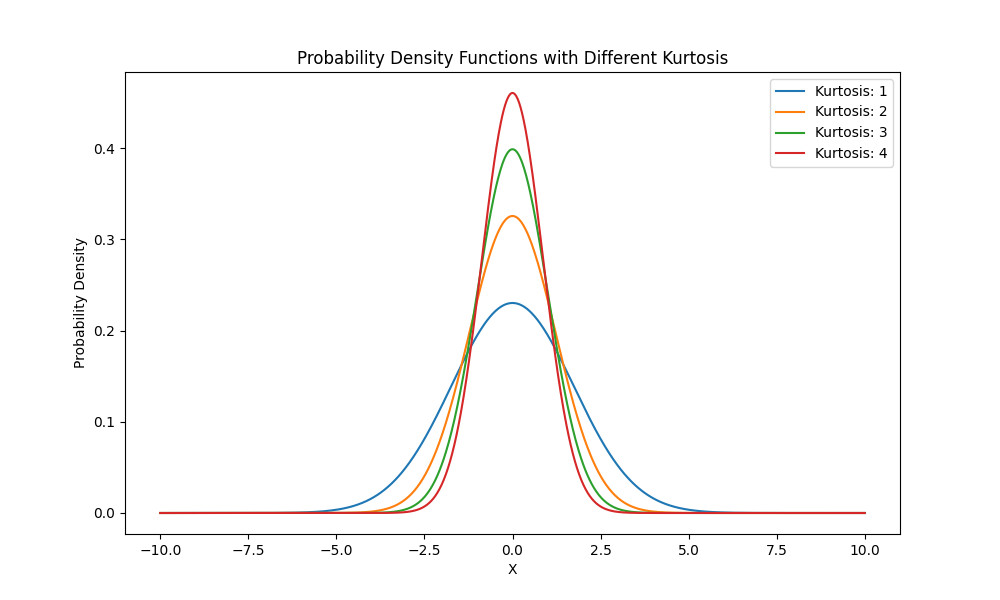
意义解释： 样本的偏度与峰度其实本质上就是三阶矩和四阶矩的区别，对于三阶矩，由于是奇数阶矩如果数据左偏，那么其为小于0显然，反之大于0。而偏度绝对值的大小，则反映了偏移程度的大小。 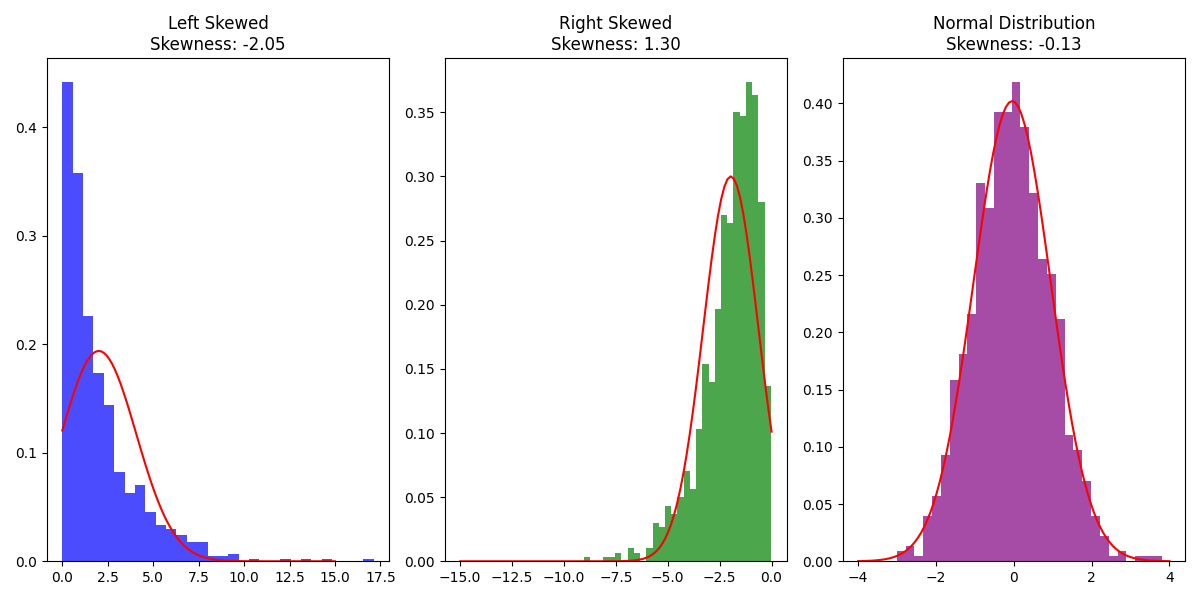对于峰度而言，可以看做样本距离$\mu$的平方除以方差的平方，他们峰度越大，其实反应的问题就是数据尾部的厚度，也就是说，尾部越厚，那么峰度就会越大，并且我们会以正态分布的峰度3为标准，因此公式最后会减去3.

正态分布$k$阶矩

为了后面做题需要，以及证明前面提到的正态分布峰度为3，我这里给出正态分布的$k$阶矩的算法。

$$E[(\frac{x-\mu }{\sigma }{)}^n]=(n-1)!!$$

其中$n$为偶数，因为不难看出当奇数情况时，由于标准正态分布的密度函数为偶函数，并且积分区域关于y轴对称，则奇数情况自然期望为0。

证明：

不失一般性，假设$X$服从标准正态分布，否则取$Y=\frac{x-\mu }{\sigma }$ 即可

$$\begin{array}{c}\begin{array}{rl}E[x^{2k}]& ={\int }_{-\infty }^{\infty }\frac{x^{2k}}{\sqrt{2\pi }}\exp \{-\frac{x^2}{2}\}dx\\ \text{令 }{x}^2& =2t\\ E[x^{2k}]& ={\int }_0^{\infty }\frac{2^{k-1}}{\sqrt{\pi }}{t}^{k-1}\exp \{-t\}dt\\ \text{则对于 }& \frac{2^{k-1}}{\sqrt{\pi }}\Gamma (k+\frac{1}{2})，\text{将}{2}^{k-1}\text{分配给}\Gamma (k+\frac{1}{2})\text{中前}k-1\text{个累乘}\\ \text{又由于 }& \Gamma (\frac{1}{2})=\sqrt{\pi }\\ \text{则}\frac{2^{k-1}}{\sqrt{\pi }}& \Gamma (k+\frac{1}{2})=(2k-1)(2k-3)\dots 1=(n-1)!!\end{array}\end{array}$$

证明的思路有很多，也可先求出矩母函数，再利用幂级数展开后求导进行计算，证明过程相差不大，这里留给读者自行证明。 当然，其实最朴实的想法就是求出矩母函数后，直接求n阶导数，但是那样就需要用到高阶导数的知识，比如莱布尼兹公式，或者有足够强的数学直觉直接归纳证明，这里我也不再给出证明，有兴趣的读者可以自行尝试。