👨‍💻Zhenry's Notebook Set

Search

SearchSearch

数据结构笔记6-栈和队列-栈

Nov 21, 20248 min read

参考网课数据结构-青岛大学-王卓-第五周

参考书籍《数据结构C语言版第二版》 中国工信出版集团 人民邮电出版社出版 严蔚敏 编著

定义

栈：插入和删除只能在一端进行。先进后出

队列：插入在一端，删除在另一段。先进先出

Note

插入的位置标号是指在插入完成之后，被插入元素所在的位置。

案例-进制转换 | 括号匹配

进制转换：利用的是先进先出的特性调换了结果的顺序。 括号匹配：利用先进先出的特性实现括号配对验证。

案例-表达式求值

算数表达式的构成：操作数（常，变量），算术运算符（-，+，=），界限符（括号，#）。后两者统称为算符。

表达式求值的流程——算符优先算法

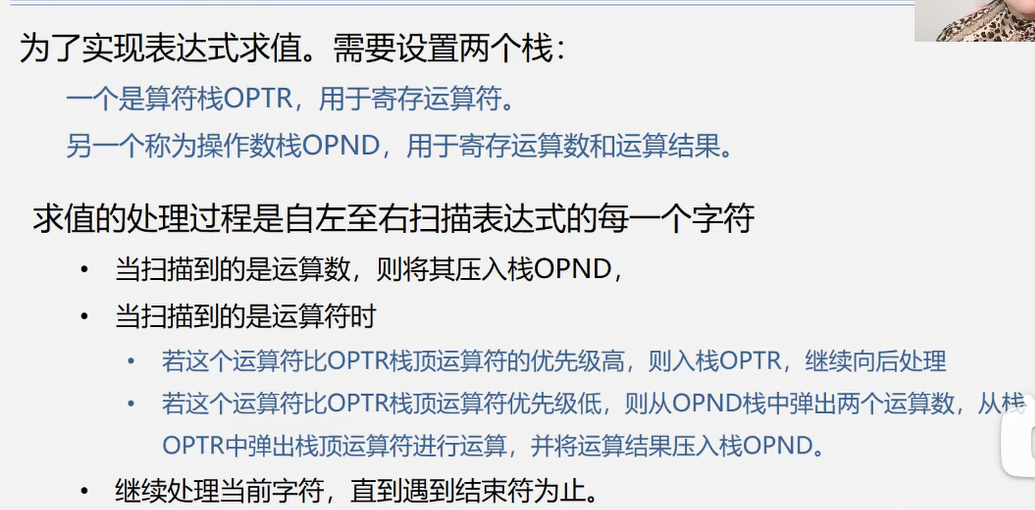
算符优先级的比较的具体过程更复杂，在此略过。

栈的抽象数据类型定义

数据对象

数据关系

规定为栈顶，为栈底。

插入和删除都在栈顶进行。

基本操作

  • 初始化
  • 销毁
  • 判断是否为空
  • 求长度
  • 取栈顶元素
  • 栈置空
  • 入栈，推入
  • 出栈，弹出

栈的表示和实现

顺序栈的表示与实现

top指针，指示栈顶元素在栈中的位置。

Hint

为了方便操作，实际上的top指针会指向栈顶元素 之上的 元素的 地址

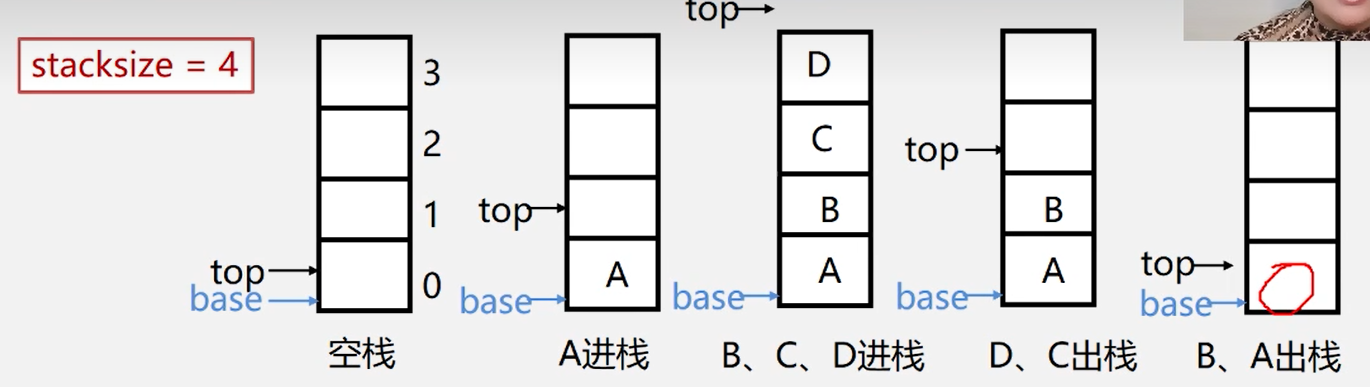
stacksize表示栈可以使用的最大容量。

base指针，指示栈底元素在栈中的位置。

空栈标志：base == top

栈满：top-base == stacksize

栈的上溢出：栈以压满还要压入。top指针指向超过了stacksize的地址。一般认为是错误，需要处理。

栈满时候的处理方法：分配更大空间作为新栈，进行移入。

栈的下溢出：没有元素了还要弹出。常用作结束条件。

顺序栈的数据结构定义

# define MAXSIZE 100
typedef struct{
	SElemType *base;
	SELemType *top;
	int stacksize;
}SqStack;

顺序栈的初始化(构造一个空栈)

Status InitStack(SqStack &S){
	S.base = new SElemType[MAXSIZE];
	//S.base = (SElemType*)malloc(MAXSIZE*sizeof(SElemType));
	if(!S.base)exit(OVERFLOW); //栈分配失败的情况
	S.top = S.base;
	S.stacksize = MAXSIZE'
	return OK;
}

顺序栈判断是否为空

Status StackEmpty(SqStack S){
	if(S.top == S.base)
		return TRUE;
	else
		return FLASE;
}

求顺序栈长度

int StackLength(SqStack S){
	return S.top-S.base;
}

清空顺序栈

Status ClearStack(SqStack S){
	if(S.base)S.top=S.base;
	return OK;
}

销毁顺序栈

Status DestroyStack(SqStack &S){
	if(S.base){
		delete S.base;
		S.stacksize=0;
		S.base=S.top=NULL;
	}
	return OK;
}

顺序栈的入栈

Status Push(SqStack &S, SELemType e){ //S是栈的名字，e传入的是入栈元素的值
	if(S.top-S.base == S.stacksize)
		return ERROR;
	*S.top++=e;  //简化写法参考下面笔记
	return OK;
}

*S.top++=e等价于*S.top=e;S.top++

顺序栈的出栈

Status Pop(SqStack &S, SElemType &e){
	if(S.top==S.base)  //等价写法`if(StackEmpty(S))`
		return ERROR;
	e=*--S.top;  //指针先下移，之后再取出
	return OK;
}

链栈

链栈的类型定义

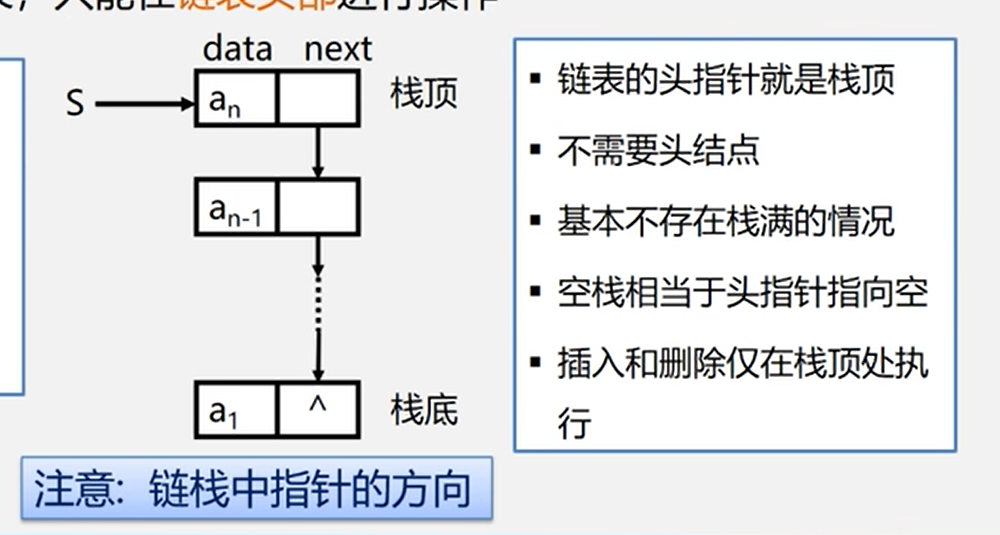
运算受限制的单链表，只能在链表的头部操作，类似单链表的定义，有自己定义自己的特征

typedef struct StackNode{
	SElemType data;
	struct StackNode *next;
}StackNode, *LinkStack;
LinkStack S;

Note

S是栈的头指针，指向栈顶元素，也就是最后进来的那个元素，是用来索引栈的标识。

链栈的特点

链栈的初始化

void InitStack(LinkStack &S){
	S=NULL;
	return OK;
}

链栈是否为空

Status StackEmpty(LinkStack S){
	if(S==NULL) return TRUE;
	else return FALSE;
}

链栈的入栈

Status Push(LinkStack &S, SElemType &e){
	p=new StackNode;
	p->data=e;
	p->next=S;
	S=p;
	return OK;
}

链栈的出栈

Status Pop(LinkStack &S, SElemtype &e){
	if(S==NULL) return ERROR;
	e=S->data;
	p=S;
	S=S->next;
	delete p;
	return OK;
}

取栈顶元素

SElemType GetTop(LinkStack S){
	if(S!=NULL)
		return S->data;
}

栈和递归

递归相关的定义

递归的定义：一个对象部分的包含他自己，或者用他自己定给自己定义，则称这个对象是递归的。

递归过程：一个对象直接的或者间接的调用自己，则称这个过程是递归的过程。

例如，求阶乘函数：

long Fact(long n{
	if(n==0) return 1;
	else return n*Fact(n-1);
}

常见的递归设计：

  1. 数学中的递归数列：阶乘函数，斐波那契函数
  2. 具有递归特性的数据结构：二叉树，广义表
  3. 可递归求解的问题：迷宫问题，汉诺塔问题

递归问题的“分治法”求解条件

  1. 能讲一个问题转换为一个新问题，且新问题的解法和原问题类似。
  2. 上述转化可以使问题简化。
  3. 有明确的递归出口，即递归边界
void p(参数){
	if(递归结束条件) 可直接求解； ---基本项
	else p(较小的参数)； ---归纳项
}

补充-函数的调用过程

调用函数前系统要完成：

  1. 将实参，返回地址，传递给被调用函数
  2. 为被调用函数的局部变量分配储存区
  3. 将控制转移到被调用函数的入口（对程序的控制权转移到被调用函数）

调用函数后系统要完成：

  1. 保存被调用函数的计算结果
  2. 释放别调用函数的数据存储区
  3. 依照被调用函数保存的返回地址，将控制转移到主调函数

当多个函数进行了嵌套调用：（通过栈来实现）

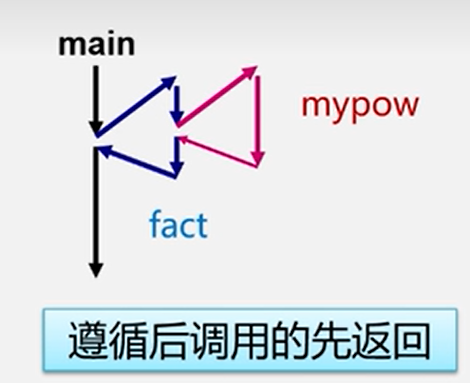
递归调用的实现

递归工作栈——在递归程序运行期间使用的数据存储区

工作记录——实参，局部变量，返回地址

递归的优缺点

优点：结构清晰，程序易读

缺点：每次都要实现工作记录，入栈时候要保存状态信息，出栈时候要恢复状态信息。时间开销大。

解决方法：递归非递归，提高时间效率

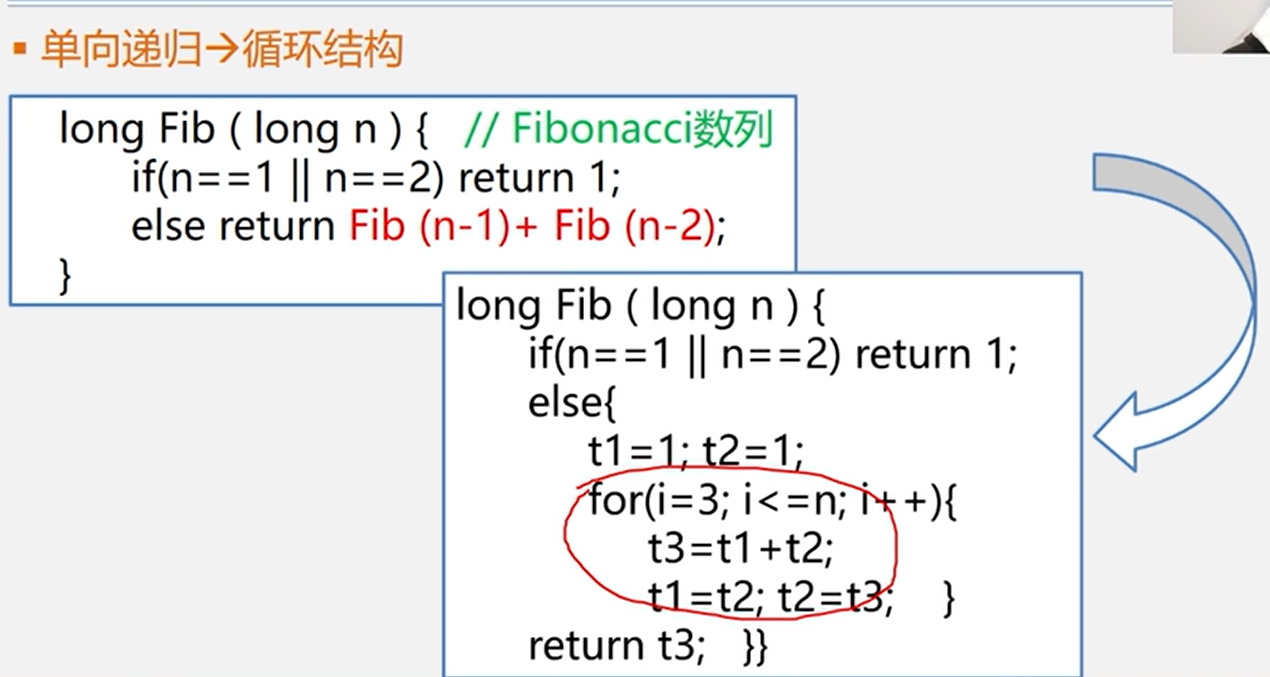
  • 尾递归，单向递归循环结构，详见下方例子A。
  • 自己进行特殊栈的设计——自用栈模拟系统的运行时栈，了解即可。

例子A

Graph View

Backlinks